Full Moon Cycle
Author: Dr A.R. (Tom) Peters,
©2003, ©2021, ©2022 Dr A.R. (Tom) Peters
Note:
Derived from "Wikipedia: Full moon cycle"
This article was initally written from 2003 for Wikipedia by me (Tom Peters) and Karl Palmen. It was deleted on 21 July 2017 because it contains too much "original research". I have been hosting it on my personal website since 24 February 2021.
The Full Moon Cycle (FMC) is a cycle of about 14 lunations over which full moons vary in apparent size and age (time since new moon). The sequence is as follows:
- big full moon (perigee at full moon)
- young full moon (perigee at first quarter)
- small full moon (perigee at new moon)
- old full moon (perigee at last quarter)
Contents
Explanation
The apparent size of the Moon varies because the orbit of the Moon is elliptical, and as a consequence at one time it is nearer to the Earth (at perigee) when it appears larger than half an orbit later (at apogee) when it appears smaller. The orbital period of the Moon from perigee to apogee and back to perigee is called the anomalistic month, and has a duration of about 27.5 days.
The appearance, or phase, of the Moon is due to its motion with respect to the Sun as seen from the Earth. It varies in a period of time called a lunation, also called synodic month; its duration (about 29.5 days) is 2 days longer than an anomalistic month. The age is the number of days since new moon.[1]
As a consequence the apparent diameter of a full moon varies depending on when it occurs in the anomalistic month: larger near the Earth (near perigee); or smaller when more distant (near apogee); see the image.

Comparison of the apparent size of full moon at perigee and at apogee; note that the photos have been taken 7 lunations apart, which equals half a Full Moon Cycle. (from Wikimedia)
Also, like for all celestial bodies, the speed of the Moon varies in its elliptic orbit: faster near perigee, and slower near apogee. So the time of the half lunation between a new moon and the next full moon varies, depending on where in the elliptical orbit it begins, and so affects the age of the full moon.[2]
The Full Moon Cycle (FMC) is somewhat less than 14 synodic months and somewhat less than 15 anomalistic months. Its significance is that when you start with a full moon at the perigee - which appears large - then subsequent full moons will occur ever later after the passage of the perigee: after 1 FMC, the accumulated difference between the number of completed anomalistic months and the number of completed synodic months is exactly 1, and the full moon occurs again at perigee, giving a large apparent moon.
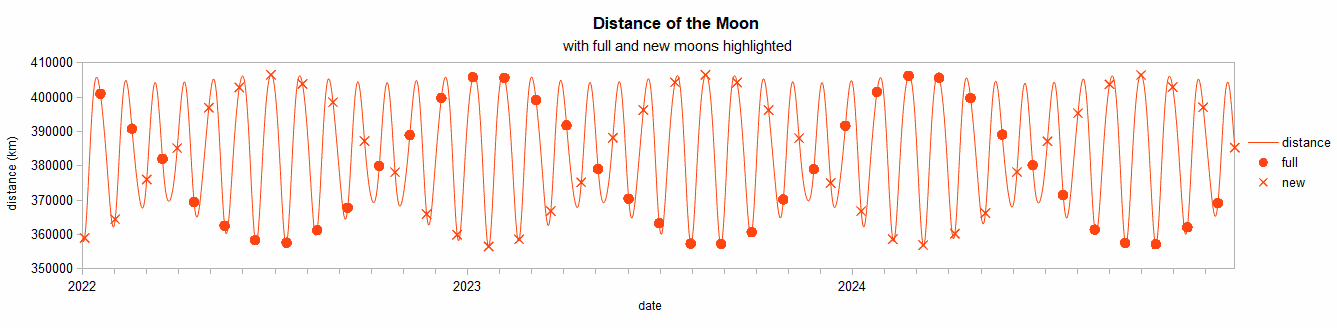
Variation of the distance of the Moon from Earth. Full and new moons are indicated by symbols. Note that every 14th full moon is near perigee (least distance, at the bottom). (from Wikimedia)
The average duration of the anomalistic month is:
- AM = 27.55454988 days [3]
The synodic month has an average duration of:
- SM = 29.530588853 days [4]
The FMC is the beat period of these two, and has a duration of:
- FMC = (SM×AM)/(SM−AM) = 411.78443d = 13.944335 SM
The Full Moon Cycle and the year
Formulated in another way: the FMC is the period that it takes the Sun to return to the perigee of the Moon's orbit (as seen from the Earth). So it is a kind of "perigee year", similar to the eclipse year which is the time for the Sun to return to the ascending node of the Moon's orbit on the ecliptic.
Why does a FMC last almost 14 lunations rather than just the (365.25/29.53 =) 12.37 lunations of a year? This would be the case if the moon's orbit kept a constant orientation with respect to the stars. Instead the tidal effect of the Sun causes the orbit to precess full circle in just under 9 years. In that time the number of FMCs passed becomes 1 less than the number of sidereal years passed. See nodal precession.
The eclipse website of Fred Espenak also explains all this in a different way.
Matching synodic and anomalistic months
The equivalence of the FMC to 14 synodic months is an approximation that will accumulate an error of one synodic month after 18 cycles:
- 18×FMC = 251×SM = 269×AM
- whereas 18×14 = 252
The equality of 269 anomalistic months to 251 synodic months was already known to Chaldean astronomers (see Kidinnu).
A good longer period spans 55 FMCs or rather 767 synodic months, which is not only close to an integer number of anomalistic months, but also is close to an integer number of days and an integer number of years:
- 767×SM = 822×AM = 55×FMC = 22650 days = 62 years + 5 days
There are 13.944335 synodic months in a FMC, the 251-month cycle approximates the FMC to 13.944444 synodic months and the 767-month cycle approximates the FMC to 13.9454545 synodic months.
The Full Moon Cycle and the saros - using the FMC for predicting eclipses
The saros is an eclipse cycle of 223 synodic months = 239 anomalistic months = 242 draconitic months. This is also close to 16 FMCs. The circumstances of an eclipse depend much on the apparent size of the Moon, and therefore on its phase in its anomalistic cycle and consequently in its FMC. In the duration of a saros cycle there are about 40 eclipses. 1 saros after an eclipse, another eclipse is very likely to occur that much resembles that first eclipse. Moreover, eclipses that occur a multiple of FMCs apart are also very similar. This may have been known to the ancient Greeks: in the Antikythera mechanism the saros cycle is represented in a dial arranged as a 4-turn spiral, which also has quadrant divisors on its inside. It has been proposed (Freeth et al. 2008) that this matches a division of the saros in 16 FMCs, and may have been used to predict the appearance of eclipses.
Using the Full Moon Cycle for predicting new and full moons
Besides predicting when a full moon will be large, the FMC can be used to more accurately predict the exact time of the full moon or new moon (together called: syzygies).
Mean syzygy
First we have to find the moment of mean syzygy, before we can correct it with our FMC correction. Polynomial expressions are given on another page: New Moon.
Instead of working with full polynomials we can use a linear approximation. And instead of computing with decimals, we approximate the lunation length by a simple fraction.
The period of the mean synodic month can be approximated as 29 + 26/49 days. A more accurate fraction is 29 + 451/850. The lunation length from Babylonian tradition, still used in the Hebrew calendar, can be expressed as 29 + 13753/25920 days.
It is sufficient to keep track of just the numerator by adding once every lunation an integer constant to a variable that we shall here name the accumulator. This is similar to calculating the molad in the Hebrew calendar. It works as follows:
We maintain a variable called the accumulator which essentially is the time of day that the mean syzygy falls. In our case, using the approximate lunation length of 29 + 26/49 days, its unit is 1/49 of a day. So for one lunation to the next we add 29 days, and we add 26 to the accumulator. Whenever the accumulator reaches 49 or higher a day is filled, so the syzygy falls 1 day later and we subtract 49 from the accumulator.
Because of the error in this approximation by a fraction, and because of the higher-order terms in the polynomial for the moment of mean syzygy, the accumulator needs to be corrected by subtracting 1 once every 65 years or so. At this time resolution of 1/49 day (about half an hour), the distinction between the Universal Time (UT) and Terestrial Time (TT) scales is negligable around the present time.
Periodic corrections
The Moon's phases do not repeat very regularly: the time between two similar syzygies may vary between 29.272 and 29.833 days (see New Moon for a detailed account). The reason is that the orbit of the Moon is elliptic, its velocity is not constant, so the time of the true syzygy will differ from the mean syzygy.
The deviations of the time of true new or full moon from the mean new and full moon (which repeat at regular intervals) can be expressed as a sum of a series of sine terms, i.e. are of the form:
- C1×sin(A1) + C2×sin(A2) + C3×sin(A3) + ... ,
Where the A's are arguments that vary with time and are made from combinations of four fundamental periods that appear in the orbits of the Moon and Earth; and the C's are amplitudes that have a constant value for a particular term. There are hundreds of terms; the two major terms depend on the mean anomaly of the Moon at the time of (mean) syzygy, that is: the distance along its orbit from the perigee, which is the phase of the Moon in its anomalistic cycle. As we have seen, this anomalistic cycle coincides with the synodic cycle again after 1 FMC.
The three largest terms for the computation of true phase from mean phase are (from Meeus 1991, ch. 47 p. 321):
| Amplitude for New Moon | Amplitude for Full Moon | Argument | Meaning of the argument |
|---|---|---|---|
| −0.40720 | −0.40614 | M' | mean anomaly of Moon |
| +0.01608 | +0.01614 | 2×M' | |
| +0.17241 | +0.17302 | M | mean anomaly of Sun |
Amplitudes in days; take the sine of the arguments.
Now instead of computing the actual value of M' and 2×M' and the sine terms for every new or full moon, we can use the fact that these approximately repeat every FMC. So we can make do with a short table of 14 values: one for every new or full moon in a FMC. We only need to keep track of where we are in the basic cycle of 14 lunations. This very much simplified procedure gives much more accurate predictions of the syzygies than just using the mean values, but without computing a series of sine terms at every lunation.
Full Moon Cycle correction
The first two sine terms in the table above can be evaluated together by making use of the FMC period: using the unit of 1/49 day, we should apply the following FMC corrections to the value in the accumulator for the moment of mean new or full moon:
| FMC phase (× 1/14): | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correction (× 1/49 day): | 0 | -8 | -15 | -19 | -20 | -16 | -9 | 0 | 9 | 16 | 20 | 19 | 15 | 8 |
More efficiency
It is possible to simplify the computation of the approximate time of syzygy by combining the monthly linear increment to the accumulator for the mean syzygy, with the FMC correction. When keeping a running count in an accumulator then for each successive lunation you first have to subtract the FMC correction for the previous lunation, then add the mean increment of 26, and then add the new FMC correction. That is, you have to add differential increments to the accumulator. This can be done in one step using a single table with 14 entries like before: this is possible because the FMC corrections add up to 0.
| FMC phase (× 1/14): | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correction (× 1/49 day): | 18 | 18 | 19 | 22 | 25 | 30 | 33 | 35 | 35 | 33 | 30 | 25 | 22 | 19 |
As before, the accumulator needs to be computed modulo 49 every lunation, and if it exceeds its bound then the syzygy falls a day later.
Long-term accuracy
The basic 14-lunation FMC synchronization between synodic and anomalistic months is not very accurate after running a few years, so using this basic cycle to find more accurate times of the syzygies gives decreasingly accurate results as cycles are repeated. As we have seen, the Babylonian ratio of 269/251 is a much better approximation, and it spans 18 FMCs which are equal to 18 basic 14-lunation cycles minus 1 month. So we should correct the basic cycle (of 1 FMC ~ 14 lunations) after 18 FMCs; with the proper epoch (starting date), this can be done by skipping the first entry of the first FMC (of the next large cycle of 18 FMCs), i.e. start with the second entry, with value −8 instead of 0 from the first basic 14-month table above.
When using an accumulator with the second, cyclic table above, then at the jump after 18 FMCs, first correct the accumulator by subtracting 8. Then apply the differential correction for the new FMC phase: use the value of 18 under entry 1 in the second, cyclic table above. What happens is that we skip a value of 0 for the FMC correction (under entry 0 in the first basic table above), which preserves the cyclic nature of the tables.
Solar correction
The remaining error of the predicted time of the new or full moon can be reduced again (by a factor of about 2) by taking account of the solar term (the third in the table of sine terms above). The anomalistic period of the Sun (365.259636 days) can be approximated by the calendar year (365 or 366 days; 365.2425 days on average in the Gregorian calendar). Since a calendar year has 12 or 13 new and full moons, it is sufficient to evaluate the solar term for 12 representative phases of this annual cycle, and put these in another table. The mean anomaly of the Sun currently is 0 around 2 January, so the table starts with the new or full moon closest to the beginning of January.
| Lunar month: | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Correction (x 1/49 day): | 0 | 4 | 7 | 8 | 7 | 4 | 0 | -4 | -7 | -8 | -7 | -4 | 0 |
These values must be used to correct the time of syzygy, not added to the accumulator itself.
Epochs and constants
New Moon in Jerusalem
An optimum epoch for New Moons at the meridian of Jerusalem (at 35:14:03.4 deg. East of Greenwich = +0.097873 days = 2h20m56s ahead of UT) is 29 July 1992 . That syzygy preceded the first syzygy of the current cycle of 251 New Moons, so it had the FMC correction phase 13 (in the cycle of 0 through 13) of FMC 17 (in a cycle of 0 through 17). After this the 1st FMC correction of the new cycle was dropped, and we started FMC 0 with FMC correction phase 1 . This means that the first Dark moon of 2000, on January 6, was phase 8 (in the cycle from 0 to 13), of FMC 6 (in a cycle from 0 to 17). The value of the accumulator at that time was 34, the FMC correction was +9, and the solar correction was 0 . So the New Moon occurred at (34+9)/49 = 0.88 days after local midnight, or at 0.78 days UT. The true time of New Moon was 18:14 UT = 0.760 days: an error of 0.02 days = 0.5 hours.
in short:
| epoch | first New Moon in cycle | first New Moon in 2000 | |
|---|---|---|---|
| date | 1992-07-29 | 1992-08-28 | 2000-01-06 |
| FMC | 17 | 0 | 6 |
| FMC phase | 13 | 1 | 8 |
| initial accumulator | 43 | =43+26-49 =20 | 34 |
| FMC correction | +8 | -8 | +9 |
| cyclic accumulator | 43+8-49 =2 | =2 -8 +18 = 20-8 =12 | 43 |
| solar correction | -4 | -7 | 0 |
| corrected time | 2-4+49=47 | 12-7=5 | 43+0=43 |
| computed local Jerusalem time of syzygy | (47/49)×24 = 23h | (5/49)×24 = 2h | (43/49)×24 = 21h |
Full Moon in Jerusalem
To compute the date and time of Full moon the same method can be used with the same tables; but because the Full Moon comes a half cycle after the New Moon, its FMC corrections are out of phase by half a cycle from those for the New Moon. Hence its epoch is −(18/2)×14+(14/2)+0.5 = −118.5 synodic months = 9 + 7/12 years earlier: at 30 December 1982. The first Full Moon of 2000, on 21 January, had phase 1 (in the cycle from 0 through 13) of FMC 15 (in a cycle from 0 to 17); the value of the accumulator at that time was 23, the FMC correction was −8, and the solar correction was +4. So the Full Moon occurred at (23−8+4)/49 = 0.39 days after local midnight, or at 0.29 days UT. The true time of Full Moon was 4:41 UT = 0.195 days: an error of less than 0.1 days, or 2.3 hours.
Note: there was a total lunar eclipse at that time.
| epoch | first Full Moon in cycle | first Full Moon in 2000 | |
|---|---|---|---|
| date | 1982-12-30 | 1983-01-28(/29) (*) | 2000-01-21 |
| FMC | 17 | 0 | 15 |
| FMC phase | 13 | 1 | 1 |
| initial accumulator | 25 | =25+26-49 =2 | 23 |
| FMC correction | +8 | -8 | -8 |
| cyclic accumulator | 25+8 =33 | =33 -8 +18 = 2-8+49 =43 | 15 |
| solar correction | 0 | +4 | +4 |
| corrected time | 33+0=33 | 43+4=47 | 15+4=19 |
| computed local Jerusalem time of syzygy | (33/49)×24 = 16h | (47/49)×24 = 23h (*) | (19/49)×24 = 9h |
(*) The Full Moon occurred on 28 January 1983 in UT, but on 29 January in Jerusalem mean local time; however the FMC and solar corrections are off from reality by about 3 hours, and put the syzygy back at 28 January in Jerusalem too.
New Moon in Greenwich
An alternative epoch for use with the prime (Greenwich) meridian is 21 January 1890. This epoch was chosen by looking for a date that satisfied the following criteria:
- Epoch is after switch from Julian to Gregorian calendar to avoid confusion in date references.
- Initial value of 26/49 accumulator should be zero.
- Adjustment to this accumulator by phase should be zero.
- Calculated error (difference between actual dark moon and calculated value in 49th days) should be minimal at the epoch.
21 January 1890 is the first date to match these criteria. The next date to match the criteria is 1 January 2120. The former is chosen because it is in the past.
The actual dark moon for that date occurred at 23:49 UT the previous day, 11 minutes earlier than the epoch.
| epoch | first New Moon in cycle | first New Moon in 2000 | |
|---|---|---|---|
| date | 1890-01-21 | 1891-02-08 | 2000-01-06 |
| FMC | 17 | 0 | 6 |
| FMC phase | 0 | 0 | 8 |
| initial accumulator | 0 | 0 + 13×26 mod 49 = 44 | 30 |
| FMC correction | 0 | 0 | +9 |
| cyclic accumulator | 0+0 =0 | 44 | 39 |
| solar correction | 0 | +4 | 0 |
| corrected time | 0+0=0 | 44+4=48 | 39+0=39 |
| computed UT of syzygy | (0/49)×24 = 0h | (48/49)×24 = 23.5h | (39/49)×24 = 19h (*) |
Explanation of calculations: the epoch is computed to fall on the start of FMC 17 (last of the 18 FMCs), so the first New Moon of the next cycle is one FMC later. Normally one FMC is 14 lunations, so the new accumulator would be 0 + 14 × 26 mod 49 = 21 . However with this epoch we choose to drop a lunation from the last, not the first FMC in the longer cycle. So the accumulator for the first New Moon is 0 + 13 × 26 mod 49 = 44 . It doesn't show up in this chart, but here we skip phase 7 , which has the associated correction of 0 . We need to discard a month with zero correction, so that we don't have to track discarded corrections.
(*) Note that the chosen lunation length of 29+26/49 days is a bit too long, so an adjustment of −1/49 day must be made periodically to compensate. An adjustment every 850 lunations (about 69 years) brings the value pretty close. In this case there has been one such adjustment between the epoch and the new moon of January 2000 .
Statistics
The following table lists the errors of the polynomial, the FMC correction, and the FMC plus solar corrections, as compared to true syzygy, for a period of 372 years = 4601 synodic = 4931 anomalistic months:
| Maximum error (hours) | RMS (hours) | % day off | |
|---|---|---|---|
| mean new moon | -14.13 | 7.51 | 26.8% |
| with FMC correction | +6.90 | 3.06 | 11.6% |
| with FMC and solar corr. | -3.86 | 1.11 | 3.9% |
| mean full moon | +14.12 | 7.49 | 27.3% |
| with FMC correction | +6.88 | 3.05 | 11.4% |
| with FMC and solar corr. | -4.02 | 1.12 | 3.9% |
- RMS: Root-Mean-Square error (a type of statistical average)
- % day off: the percentage of cases that put the computed syzygy on the wrong day
References
- (back to ref.)^ See Meeus (1981).
- (back to ref.)^ See Jawad (1993).
- (back to ref.)^ See Meeus (1991) eq. 48.1
- (back to ref.)^ See Meeus (1991) eq. 47.1
- Jean Meeus (1981): Extreme Perigees and Apogees of the Moon, Sky&Telescope Aug.1981, pp. 110..111
- Jean Meeus (1991): Astronomical Algorithms, Willmann-Bell, Richmond, Virginia. ISBN 0-943396-35-2 ; based on the ELP2000-85 lunar ephemeris.
- Ala'a H. Jawad (Roger W. Sinnott ed.) (1993): How Long Is a Lunar Month?, Sky&Telescope Nov.1993, pp. 76..77
- Jean Meeus (2002): Ch.4 The duration of the lunation pp. 19..31 in: More Mathematical Astronomy Morsels; Willmann-Bell, Richmond VA USA 2002
- T. Freeth, A. Jones, J.M. Steele, Y. Bitsakis (2008): Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism. Nature 454, 614..617; supplementary material p.26 and p.41 (PDF) (^ back to quote)
- Fred Espenak: Eclipses and the Moon's orbit